| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- BFS
- 창의충전소
- web view
- 상속 관계 매핑
- 티스토리챌린지
- 휴대폰 기기
- 폴더구조
- 이영직
- 해외 대외활동
- springboot
- 자료구조
- 원복
- react
- 완전탐색
- 백준 1992
- 오블완
- service 테스트
- bfs dfs
- 노마드코더
- multipart upload
- 경우의 수
- ReactNative
- React Natvive
- Navigation
- 비트마스킹
- Project Bee
- FlatList
- 구현
- 버튼 활성화
- React Native
- Today
- Total
유미의 기록들
[알고리즘 -5] 그리디, 라인스위핑, 투포인터 본문
그리디 알고리즘 (탐욕법, Greedy Algorithm)
각 단계에서 최적이라고 생각하는 것인 지역적 최적해가 궁극적으로 전역최적해가 되는 것
즉, 여러 경우 중 선택의 순간마다 최적이라고 생각하는 것을 선택해나가면서 최종적인 해답에 도달하는 알고리즘
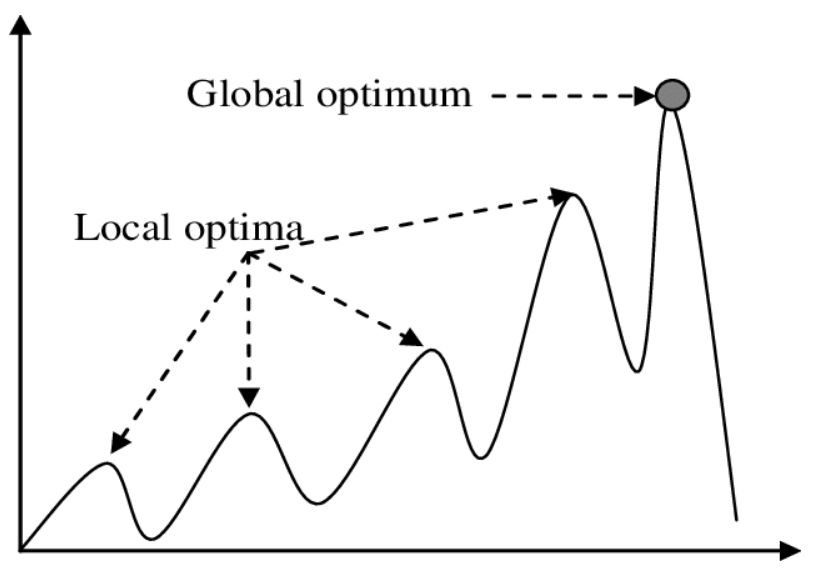
⚠️ 위 알고리즘의 문제점은 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 해서 최적의 값을 보장하는 것이 아니다. 그러나 어느정도 최적에 근사한 값을 빠르게 도출할 수 있는 장점이 있다
따라서 문제를 풀때 그리디부터 생각하기 보다 완전탐색 > DP > 그리디 순으로 생각하는 것이 좋다
그리디 알고리즘으로 최적의 해를 얻기 위한 2가지 조건
1) 최적 부분 구조를 가지고 있어야한다
지금 이상태에서 최선을 다해 선택하는 해가 결국에는 전역적인 최적해로 이어지는 구조
- 전체 문제를 작은 부분 문제로 나누어 각각의 부분 문제에서 최적의 해를 구한 후 이를 조합하여 전체 문제의 최적해를 구하는 것을 의미
2) 탐욕 선택 속성이 증명 되어야 한다
보통 귀류법으로 증명하고 앞의 선택이 이후의 선택에 영향을 주지 않는다
- 각 단계에서 가장 이상적인 선택을 하는 것이 전체적으로 최적의 결과를 가져온다는 것을 의미
2가지 조건이 성립해야 그리디 알고리즘을 적용할 수 있으며, 그리디 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다
라인스위핑 (Sweeping)

공간이나 직선 상에서 한쪽 시작점을 기준으로 반대편 종료지점까 스캔하면서 탐색하는 것만으로 점과의 집합, 선의 집합 등 탐색을 끝내는 것
📌 라인스위핑 알고리즘 문제
https://www.acmicpc.net/problem/2170
2170번: 선 긋기
첫째 줄에 선을 그은 횟수 N (1 ≤ N ≤ 1,000,000)이 주어진다. 다음 N개의 줄에는 선을 그을 때 선택한 두 점의 위치 x, y (-1,000,000,000 ≤ x < y ≤ 1,000,000,000)가 주어진다.
www.acmicpc.net

1) 두 점의 위치를 기준으로 정렬
2) 선그리기
- l = 1 , r = 4
- 시작 위치(2)가 r보다 작고 끝위치(5)가 r보다 커서 r = 5
- 시작 위치(6)가 r보다 커서
- ret = 5 - 1 = 4
- l : 6, r = 7
- ret += 7 - 6 = 5
import java.util.*;
import java.io.*;
public class Main {
static class Pair {
int from;
int to;
Pair(int from, int to) {
this.from = from;
this.to = to;
}
}
public static void main(String[] args) throws IOException{
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
List<Pair> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
StringTokenizer st=new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
list.add(new Pair(from, to));
}
list.sort(Comparator.comparingInt(a -> a.from));
int ret = 0;
int l = list.get(0).from;
int r = list.get(0).to;
for (int i = 1; i < n; i++) {
if (r < list.get(i).from) {
ret += (r - l);
l = list.get(i).from;
r = list.get(i).to;
} else if (list.get(i).from <= r && list.get(i).to > r) {
r = list.get(i).to;
}
}
ret += r - l;
bw.write(Integer.toString(ret));
bw.flush();
bw.close();
}
}
투포인터 (Two - Pointer Algorithm)
1차원 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가면서 원하는 값을 찾을 때 까지 탐색하는 알고리즘
1) 시작지점과 끝점 2개로 이루어진 투포인터 활용

2) 처음 시작점에서 같이 시작하는 투포인터 활용

📌 투포인터 알고리즘 문제
https://www.acmicpc.net/problem/3273
3273번: 두 수의 합
n개의 서로 다른 양의 정수 a1, a2, ..., an으로 이루어진 수열이 있다. ai의 값은 1보다 크거나 같고, 1000000보다 작거나 같은 자연수이다. 자연수 x가 주어졌을 때, ai + aj = x (1 ≤ i < j ≤ n)을 만족하는
www.acmicpc.net
1) 수열을 오름차순으로 정렬
→ 1 2 3 5 7 9 10 11 12
2) 시작지점과 끝점 2개의 포인터 r, l 를 잡는다
→ l = 0 , r = n - 1

import java.util.*;
import java.io.*;
public class Main {
public static void main(String[]args){
Scanner scanner=new Scanner(System.in);
int n=scanner.nextInt();
int []a=new int[n];
for(int i=0;i<n;i++){
a[i]=scanner.nextInt();
}
int x=scanner.nextInt();
Arrays.sort(a);
int l=0, r=n-1; //시작지점과 끝점 2개로 이루어진 투포인터 활용
int ret=0;
while(l<r){
if(a[l]+a[r]==x){
ret++;
l++;
r--;
}
else if(a[l]+a[r]>x){
r--;
}else if(a[l]+a[r]<x){
l++;
}
}
System.out.println(ret);
scanner.close();
}
}
'코딩테스트 기록 > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘 -6] 이분탐색, LIS (0) | 2024.04.30 |
|---|---|
| [알고리즘 -4] 비트마스킹 (0) | 2024.04.15 |
| [알고리즘 -3] 완전탐색, 백트래킹 (0) | 2024.03.13 |
| [알고리즘 -2] 깊이 우선 탐색(DFS) vs 너비 우선 탐색(BFS) (0) | 2024.02.20 |
| [알고리즘 -1] 시간복잡도, 빅오표기법, 공간복잡도 (0) | 2024.01.17 |




